COORDINATE GEOMETRY
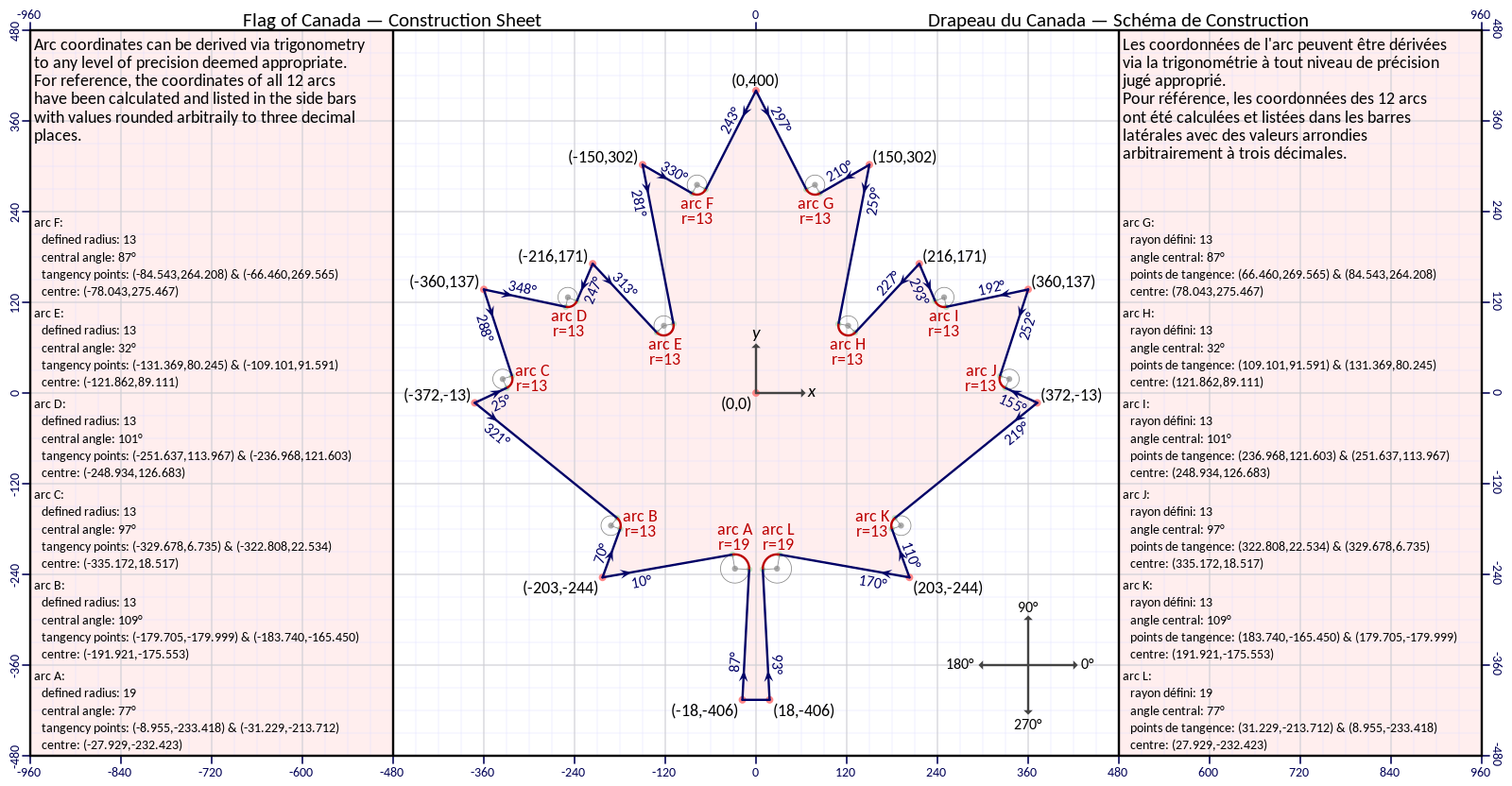
In the diagram, the flag has been plotted on a cartesian plane.
What is a cartesian plane?
A Cartesian plane is defined by two perpendicular number lines: the x-axis, which is horizontal, and the y-axis, which is vertical. Using these axes, we can describe any point in the plane using an ordered pair of numbers.
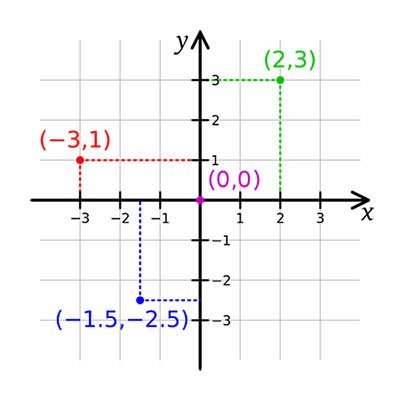
The location of a point in the plane is given by its coordinates, a pair of numbers expressed as (x,y). The first number x denotes the point’s horizontal position and the second number y denotes its vertical position. All positions are measured relative to a central point called the origin, whose coordinates are (0,0). As an example, the point (2,3) is 2 units to the right and 3 units up from the origin. Negative coordinate numbers tell us to go left or down.
In the maple leaf diagram, the flag has been plotted with the center of the flag at the origin, the point (0,0). We can further deduce the locations of various other points with a few notable observations:
- The white rectangle that the maple leaf is centred on is in fact a square with a length that is half the entire flag.
- The two red stripes are twice as long as they are wide and each take up one-quarter of the flag’s length.
- The tips of the maple leaf’s side crowns are exactly one eighth along the white square.
CIRCLE GEOMETRY
In the maple leaf diagram, we can also see circles where the various sides intersect. What this means is that instead of any two lines of the maple leaf meeting at an angle, they come together at a curve or an arc. How do we measure this arc?
This brings up a few more interesting geometrical concepts:
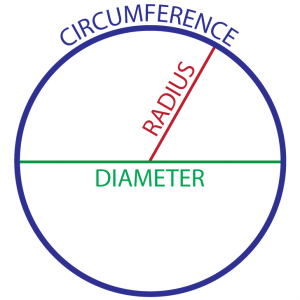
A circle’s radius (r) is the distance between the center of the circle and any point on its perimeter.
The diameter (d) of a circle is any straight line segment that passes through the center of the circle and whose endpoints lie on the circle. It is 2 x the radius of the circle.
The circumference (C) of a circle is the distance around the outside of the circle and is expressed as C = πd.
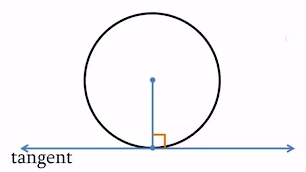
When a line is tangent to a circle at a point, it means that the line and the circle’s radius drawn to a point on the line form a 90° angle.
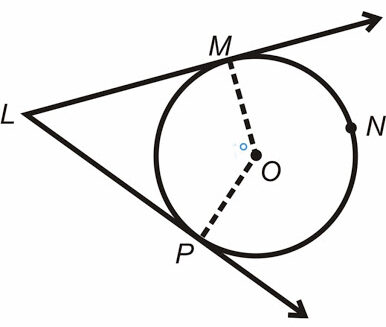
The central angle is the angle formed between the two radii that contact two points of tangency.
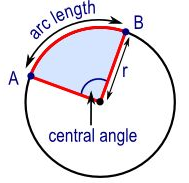
Arc length is the distance between two points along a section of a curve.
A circle is 360° all the way around; therefore, if you divide an arc’s central angle by 360°, you find the fraction of the circle’s circumference made up by the arc.
central angle
360°
Then, if you multiply the length all the way around the circle (the circle’s circumference) by that fraction, you get the length along the arc – ie the arc length. So,
Arc length = 2πr x central angle
360°

