What is a Star? : A Geometric Shape
By geometrical definition, a star is a regular polygon: simple or complex.
Remember…
Polygon – any two-dimensional shape formed with straight lines and is closed.
Regular polygon – a polygon whose sides are all the same length (equilateral) and whose angles are all the same (equiangular).
A simple polygon is an enclosed shape consisting of straight, non-intersecting lines.
A complex polygon is an enclosed shape consisting of straight lines that intersect.
A convex polygon is defined as a polygon with all its interior angles less than 180°. Otherwise, the polygon is concave.
STAR POLYGONS
A “regular star polygon” is therefore, a self-intersecting equilateral equiangular polygon. A regular star polygon is denoted by its Schläfli symbol {p/q}, where p = the amount of vertices / sides and q = the adjointment interval.
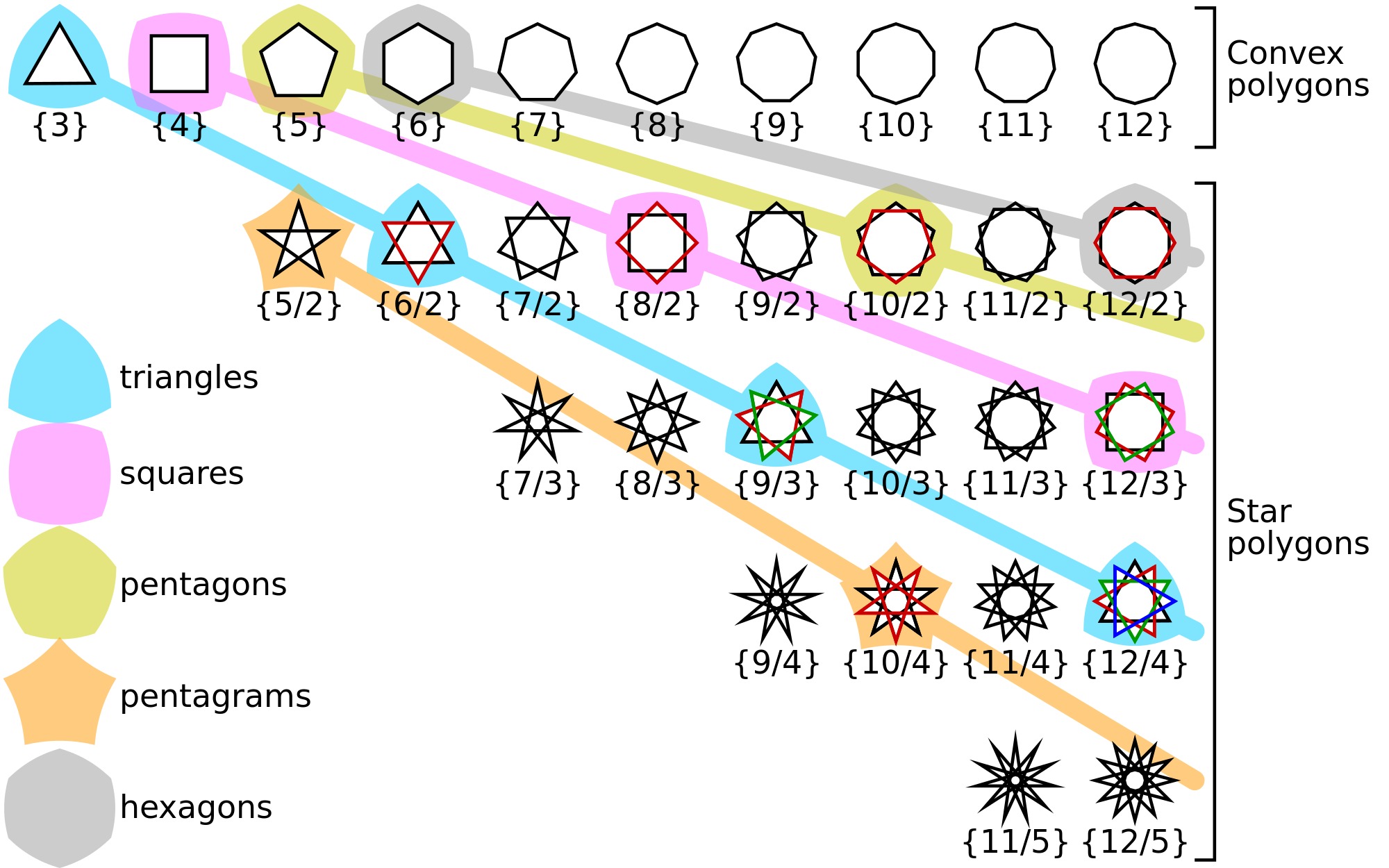
The geometry of regular star polygons was first studied systematically by Thomas Bradwardine, and then later by Johannes Kepler. Kepler defined a star polygon as an augmentation of a regular polygon, achieved by extending each side of the regular polygon until it meets a non-adjacent side, forming a vertex.
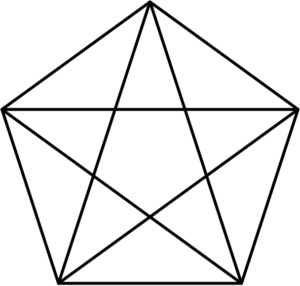
More precisely, regular star polygons can be created by connecting one vertex of a simple, regular, p-sided polygon to another, non-adjacent vertex and continuing the process until the original vertex is reached again – i.e., for integers p and q, a star polygon is constructed by connecting every qth point out of p points, regularly spaced in a circular placement.
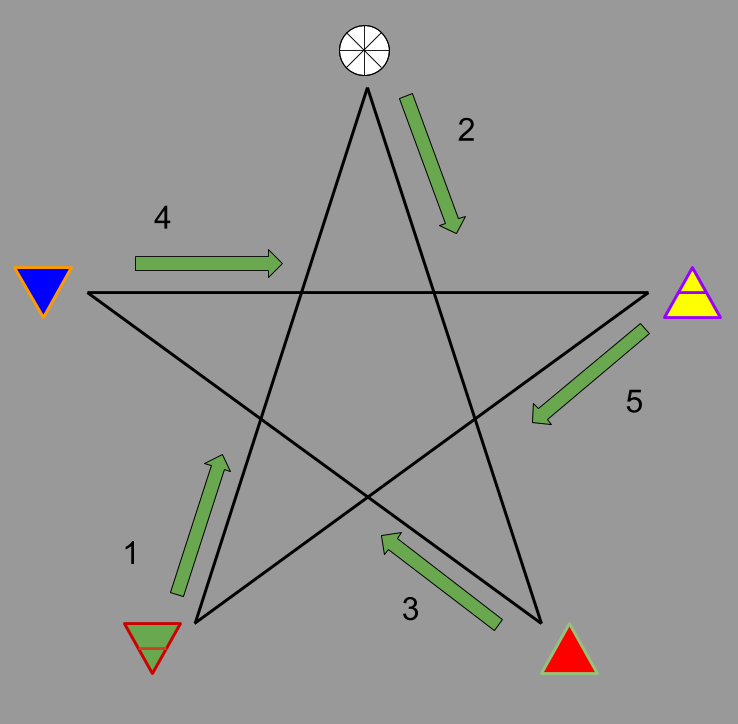
For instance, in a regular pentagon, a five-pointed star can be obtained by drawing a line from the 1st vertex to the 3rd vertex, from the third vertex to the 5th vertex, from the fifth vertex to the 2nd vertex, from the second vertex to the 4th vertex, and from the fourth vertex back to the 1st vertex. In this example, p = 5 (5 vertices / full sides) and q = 2 (every second vertex is adjoined).

