Why is it called the CIRCLE OF FIFTHS ?
There are twelve semitones in an octave. These are the white AND black notes on a piano.
In about 600 B.C.E., Pythagoras arranged the 12 notes (half-steps) of the octave around a circle in a similar manner to a clock. This depiction became known as the Pythagorean Circle.
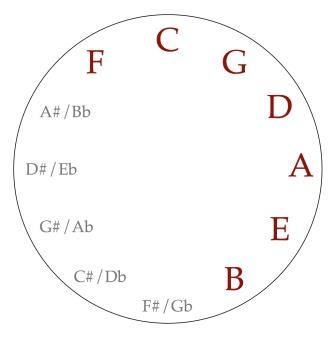
Revisions and improvements to the Pythagorean Circle were made by Nikolay Diletsky in the 1670s, and Jonn David Heinichen in 1728, resulting in the version we have today – the Circle of Fifths.
A simple way of understanding why it is called the Circle of Fifths is by looking at a piano keyboard. Start at any key, count seven keys to the right (both black and white, not including the first) and you will land on next note shown on the circles above and below.
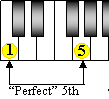
Seven half steps, the distance from the 1st to the 8th key on a piano is a “perfect fifth” (“perfect” because it is neither major nor minor, but applies to both major and minor scales and chords, and a “fifth” because, although it is a distance of seven semitones on a keyboard, it spans five adjacent notes in the major or minor scale).
So, as you move around the circle of fifths in a clockwise direction, the next note you encounter will be a fifth above the note before it.
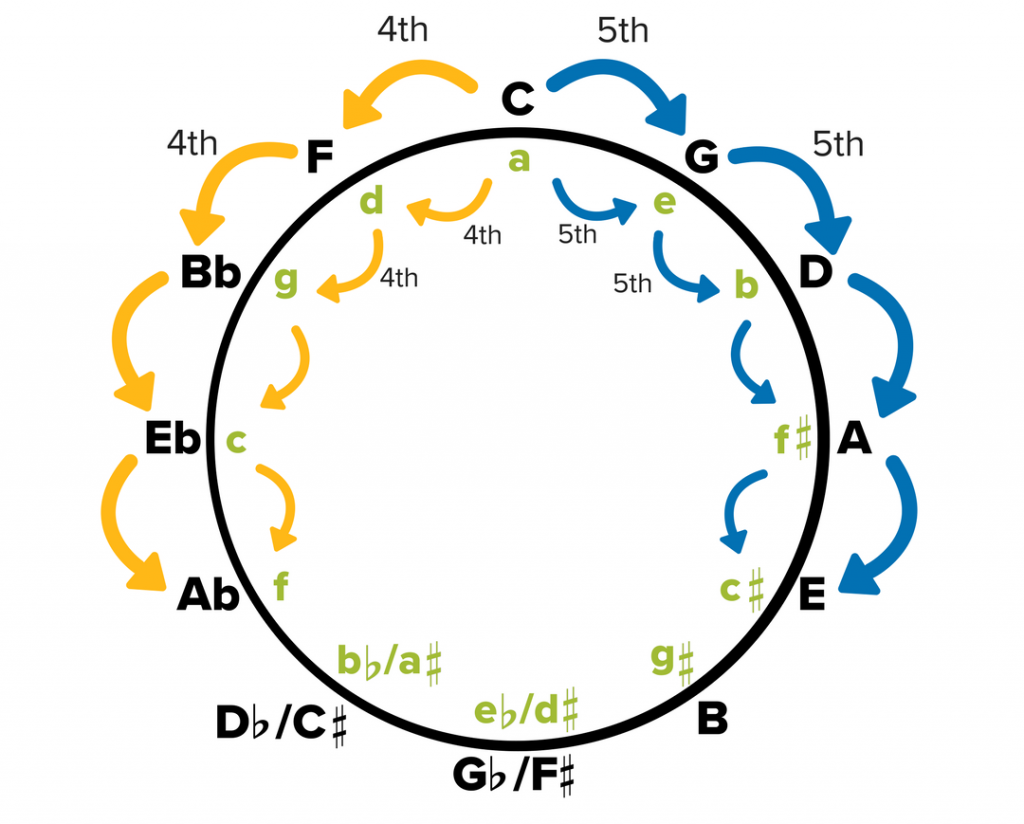
For example, starting with C, one fifth above C is G which is the fifth note of the C major scale.

Next, we have D which is the fifth note of the G major scale.
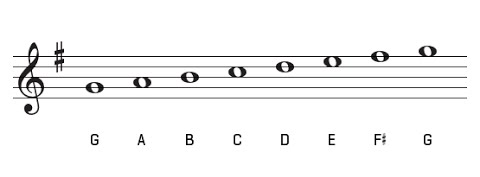
Continuing on by fifths, we have, A, E, B, F♯, C♯, A♭, E♭, B♭, F, and finally C once again.

The same applies to the minor keys (on the inner circle). Starting with A Minor, E is a fifth up from A. B is a fifth up from E. F♯ is a fifth up from B. C♯ is a fifth up from F♯, and so on.
CIRCLE OF FOURTHS, what is that?
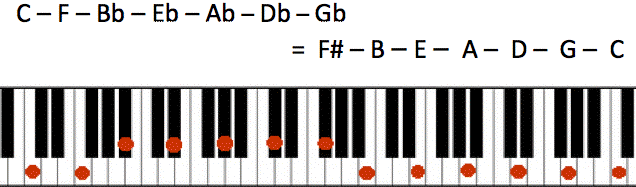
Once in a while, the Circle of Fifths might be referred to as the Circle of Fourths. This is because if you move around the circle counterclockwise, you will see the progression moves by fourths (spans four adjacent notes).

What is the Circle of Fifths used for?
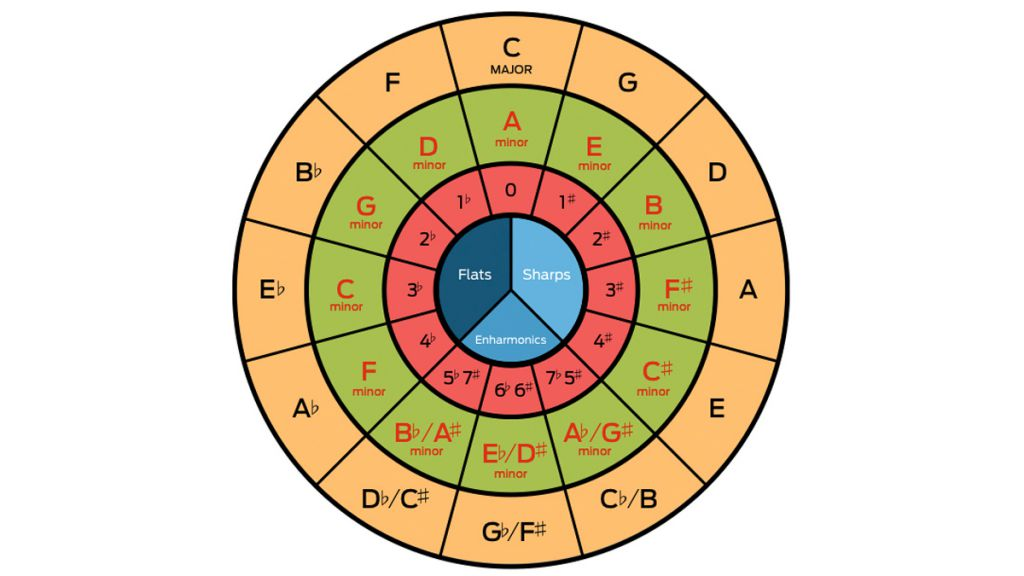
- A bit like a musical version of the periodic table, the letters can either represent notes, chords or keys.
- The circle groups together all 12 major keys with their relative minors (a relative key is defined as the minor key that uses the same notes as a particular major key, or a major key that uses the same notes as a particular minor key).
- It tells us how many sharps or flats are in each key: as you go clockwise from the top, each key adds one more sharp until you get to seven sharps (C# major); going counterclockwise from the top tells us the number of flats, adding a flat to every key until you end up at seven flats (Cb major).
- Without going into extensive detail, it also tells us what chords are available in each key, can help to transpose music into a different key, and can help to move between keys in a song.

