To better understand TESSELLATIONS, let’s review some GEOMETRY!
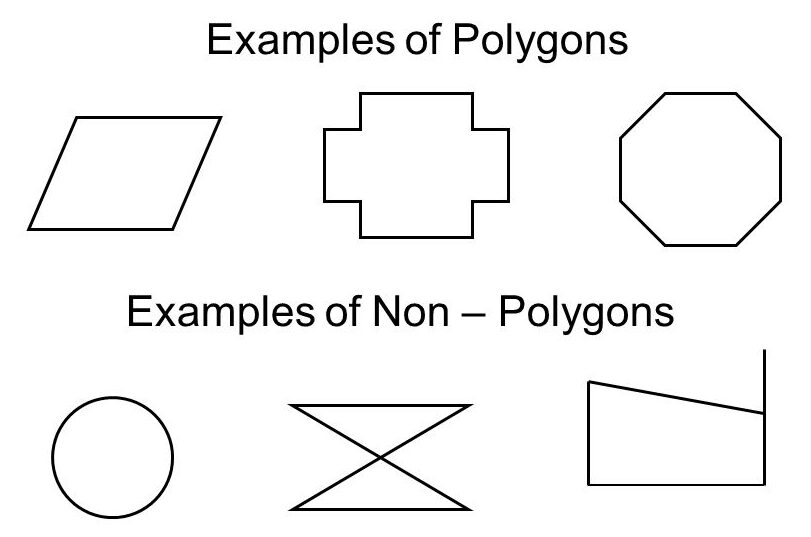
Simple Polygon – any two-dimensional shape formed with straight lines that do not intersect and and is closed.
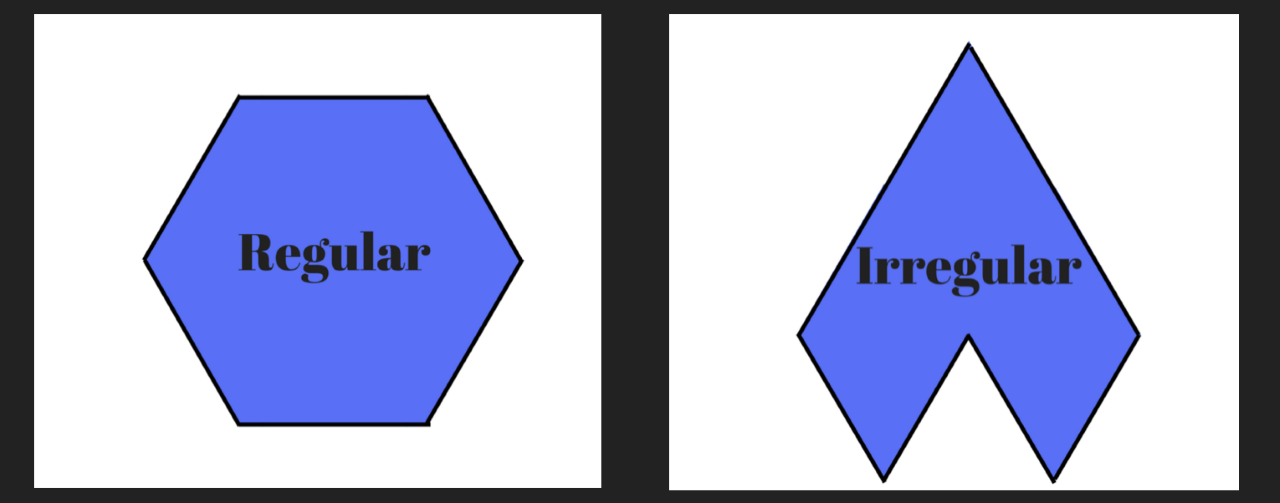
Regular polygon – a polygon whose sides are all the same length (equilateral) and whose angles are all the same (equiangular); otherwise, it is an Irregular Polygon.
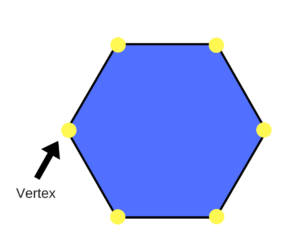
Vertex – a point where two lines meet to form an angle.
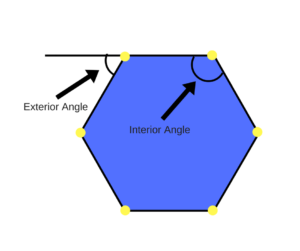
Interior angle – an angle inside a polygon at one of its vertices. The sum of the interior angles of a regular polygon is (n – 2) x 180° where n is the number of sides of the polygon. The interior angle at any vertex of a regular polygon is (n – 2) x 180° / n.
Exterior angle – an angle outside a polygon at one of its vertices.
Now that we have a better understanding of some basic geometry, let’s move onto the classification of tessellations of which there are three: regular, semi-regular and non-regular.
Regular tessellations are made up entirely of identically sized and shaped regular polygons. Every vertex looks the same and the sum of the interior angles at each vertex is 360°. Only three combinations of singular regular polygons create regular tessellations.

Let’s go through some regular polygons one by one to see why only three work and the others don’t.
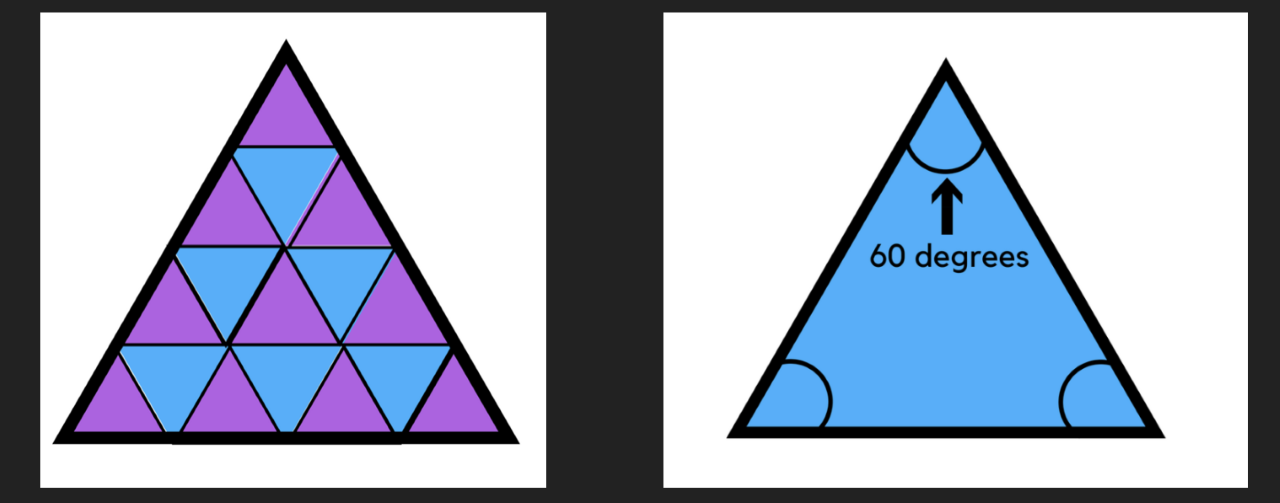
Triangles:
Notice that each vertex looks the same – has the exact same composition of shapes around it: six triangles.
The interior angle of an equilateral triangle is 60 degrees.
60 + 60 + 60 + 60 + 60 + 60 = 360
Therefore triangles tessellate.
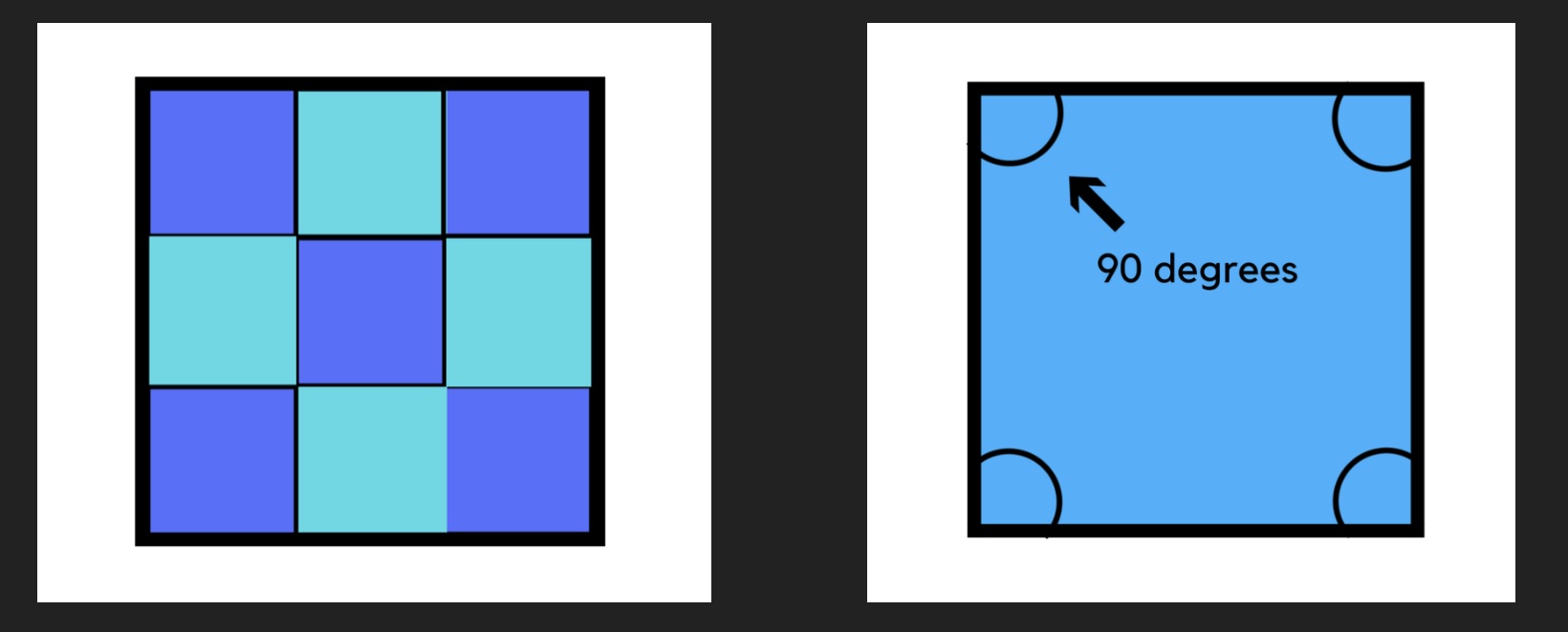
Squares:
Each vertex looks the same – has the exact same composition of shapes around it: four squares.
The interior angle of a square is 90 degrees.
90 + 90 + 90 + 90 = 360
Therefore, squares tessellate!
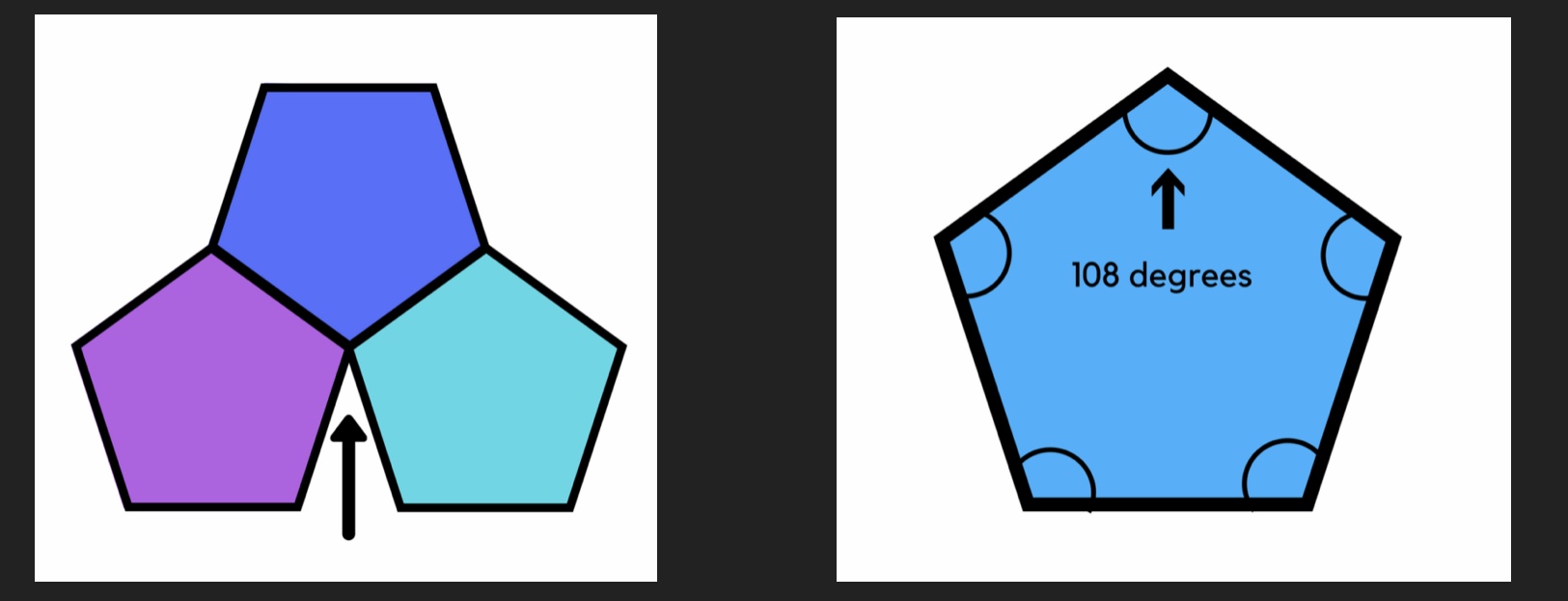
Pentagons:
Oh no! We have a gap between the pentagons!
There are three pentagons at the vertex.
The interior angle of a pentagon is 108 degrees.
108 + 108 + 108 = 324. Not 360!
Therefore, pentagons do not tessellate.
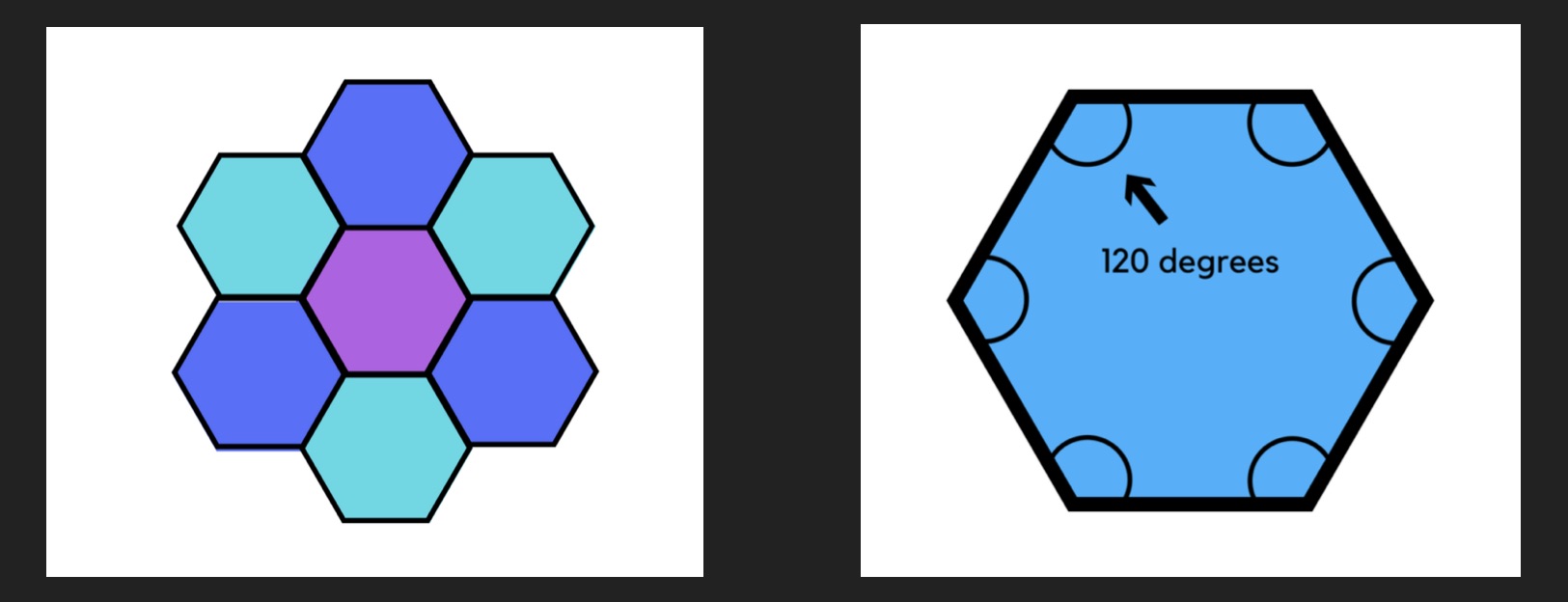
Hexagons:
Yay! Each vertex looks the same – has the exact same composition of shapes around it: three hexagons.
The interior angle of a hexagon is 120 degrees.
120 + 120 + 120 = 360
Therefore, hexagons tessellate!
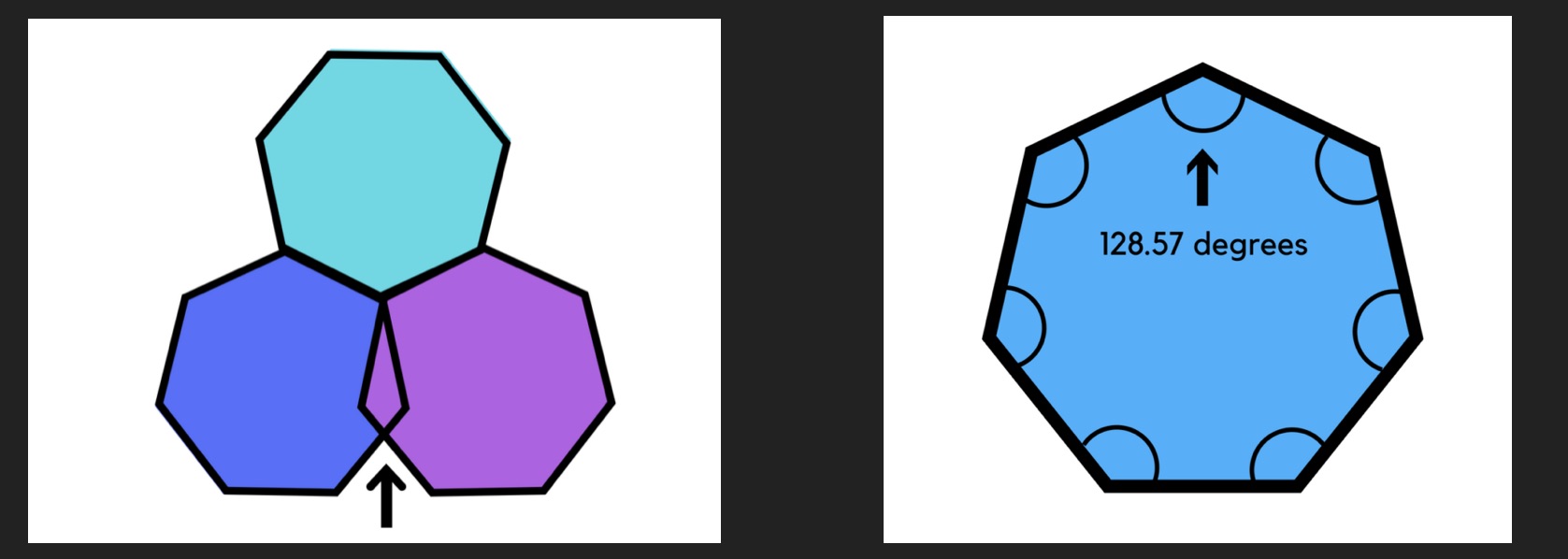
Heptagons:
Oh no! The heptagons are overlapping!
There are three heptagons at the vertex.
The interior angle of a heptagon is 128.57 degrees.
128.57 + 128.57 + 128.57 = 385.71. Not 360!
Therefore, heptagons do not tessellate.
Neither do octagons (405), or nonagons (420), or decagons (432) or in fact, any regular polygon with more than six sides. They will all overlap and therefore, will not tessellate.
Try it for yourself using the equation (n – 2) x 180° / n.
Semi-Regular tessellations are composed of 2 or more different regular polygons. Just like regular tessellations, every vertex looks the same and the sum of the interior angles at each vertex is 360°. Even more precisely, each vertex has the same pattern of polygons around it. There are only 8 combinations of different regular polygons that create semi-regular tessellations.


1. Each vertex looks the same – four triangles and one hexagon:
60 + 60 + 60 + 60 + 120 = 360.
2. Each vertex looks the same – one triangle and two dodecagons:
60 + 150 + 150 = 360.
3. Each vertex looks the same – one square, one hexagon and one dodecagon:
90 + 120 + 150 = 360.
4. Each vertex looks the same – three triangles and two squares:
60 + 60 + 60 + 90 + 90 = 360.
5. Each vertex looks the same – one square and two octagons:
90 + 135 + 135 = 360.
6. Each vertex looks the same – three triangles and two squares:
60 + 60 + 60 + 90 + 90 = 360.
7. Each vertex looks the same – two triangles and two hexagons
60 + 60 + 120 + 120 = 360.
8. Each vertex looks the same – one triangle, two squares and one hexagon:
60 + 90 + 90 + 120 = 360.
Non-Regular tessellations are composed of shapes that are not regular polygons and do not have any restrictions on their arrangement around vertices. There are an infinite number of non-regular tessellations.

Tessellations are either periodic or aperiodic. Periodic tessellations have a repeating pattern of shapes (left). Aperiodic tessellations do not have a repeating pattern of shapes (right).

Tessellations can also be referred to as Euclidean or Non-Euclidean.
Euclidean geometry is the mathematics of flat surfaces.
Non-Euclidean geometry is the mathematics of curved surfaces. Developed in the 19th century, non-euclidean geometry forced mathematicians to understand that curved surfaces have completely different rules and geometric properties compared to flat surfaces. As an example, a triangle would have different angles and line curvatures in each of the three geometries. So would squares and in fact, so would all shapes.
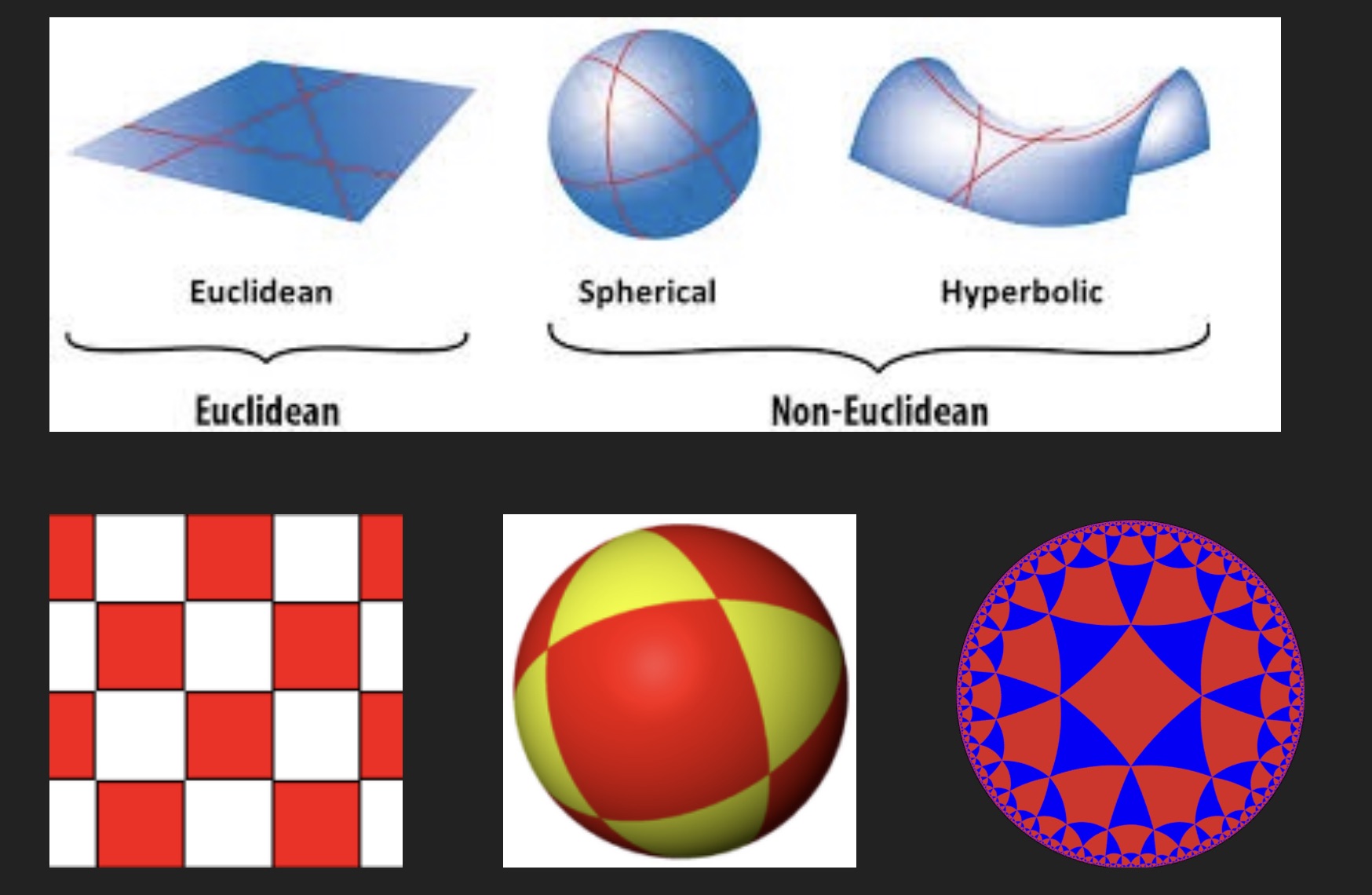
Above: Tessellating squares: Euclidean Geometry (left), Spherical Geometry (centre) and Hyperbolic Geometry (right); notice how the squares look different in each of the different geometries.
So there you have it! The not so complicated math behind tessellations!

