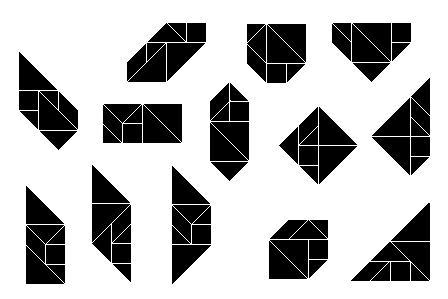
The tangram is a set of seven geometric shapes made up of five triangles, a square, and a parallelogram.
Let’s review some basic geometry!
A polygon is an enclosed, two-dimensional shape with more than two straight sides. Triangles, squares, and parallelograms are all polygons.
A TRIANGLE is a three sided polygon. The sum of the interior angles in any triangle is 180°.
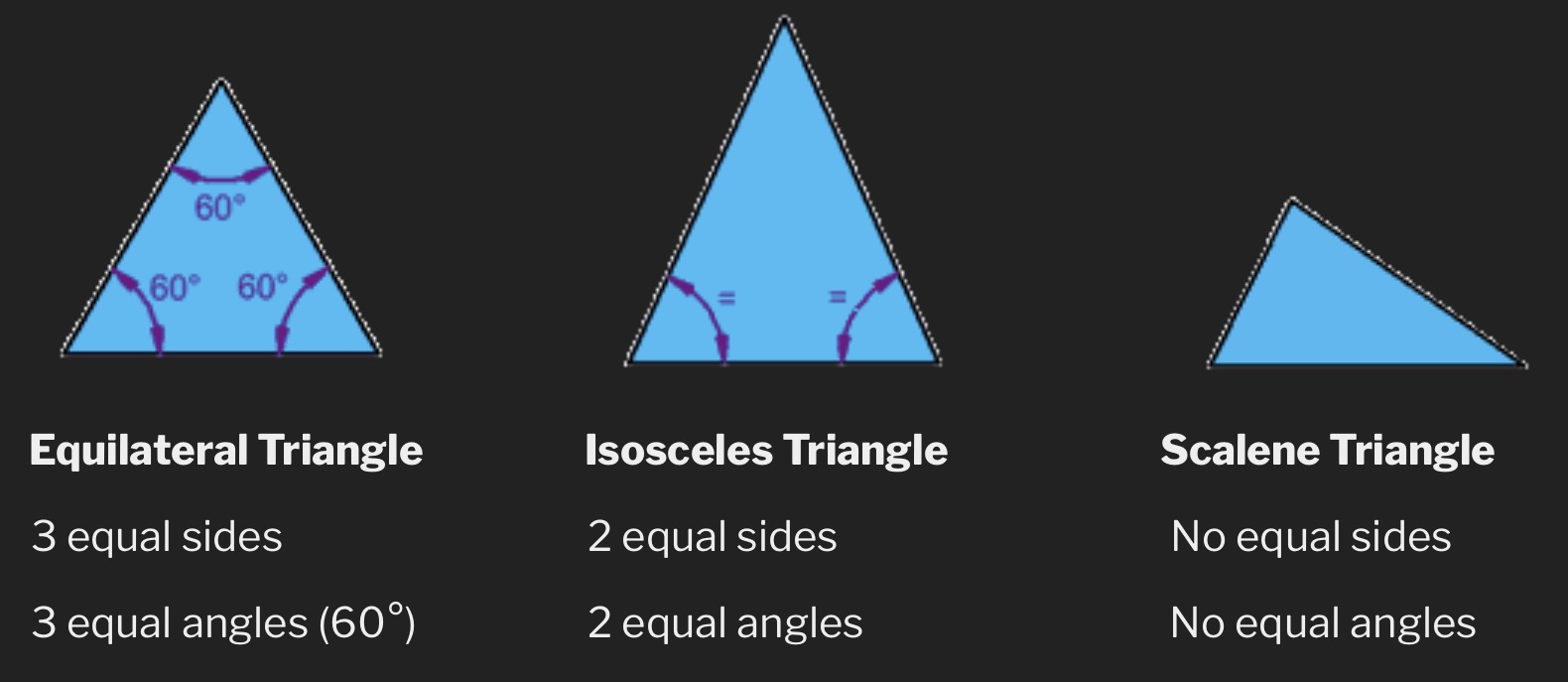
Triangles are defined by the number of their sides/angles that are equal.
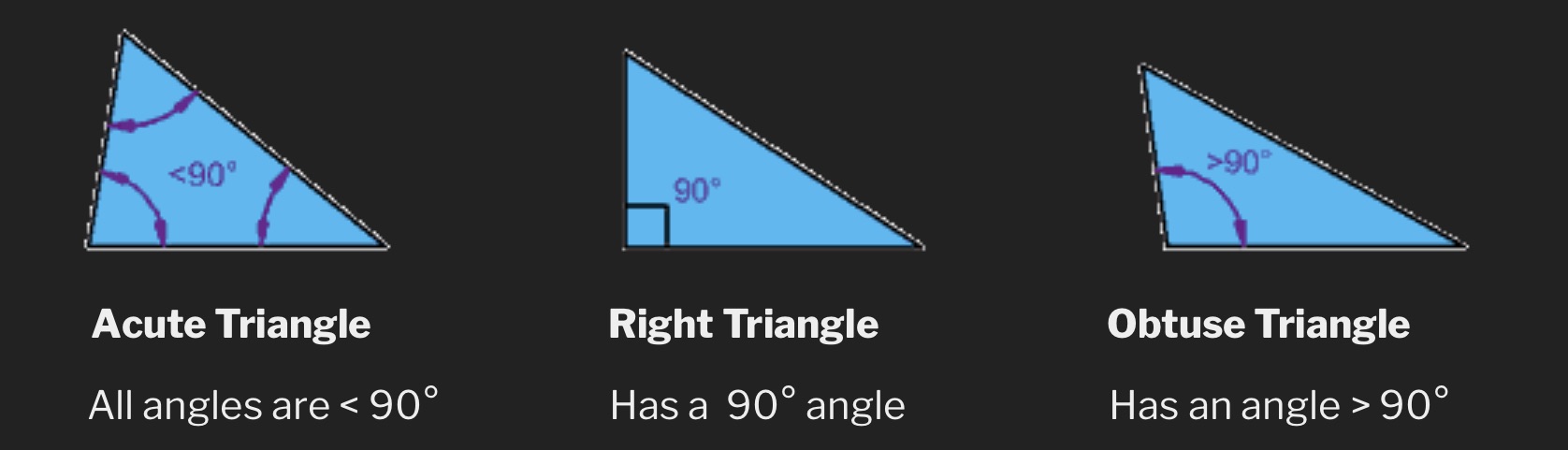
Triangles are also defined by the type of angles they have inside.
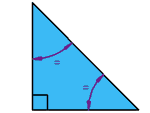
The triangles in a tangram are all RIGHT ISOSCELES TRIANGLES: 2 equal sides, 2 equal angles, and have a 90° angle. The angles of a right isosceles triangle are 90°, 45°, and 45° (total = 180°).
The Pythagorean Theorem provides us with the relationship between the sides in any right triangle. A right triangle consists of two legs and a hypotenuse. The two legs meet at the 90° angle and the hypotenuse is the longest side of the right triangle and is the side opposite the right angle.
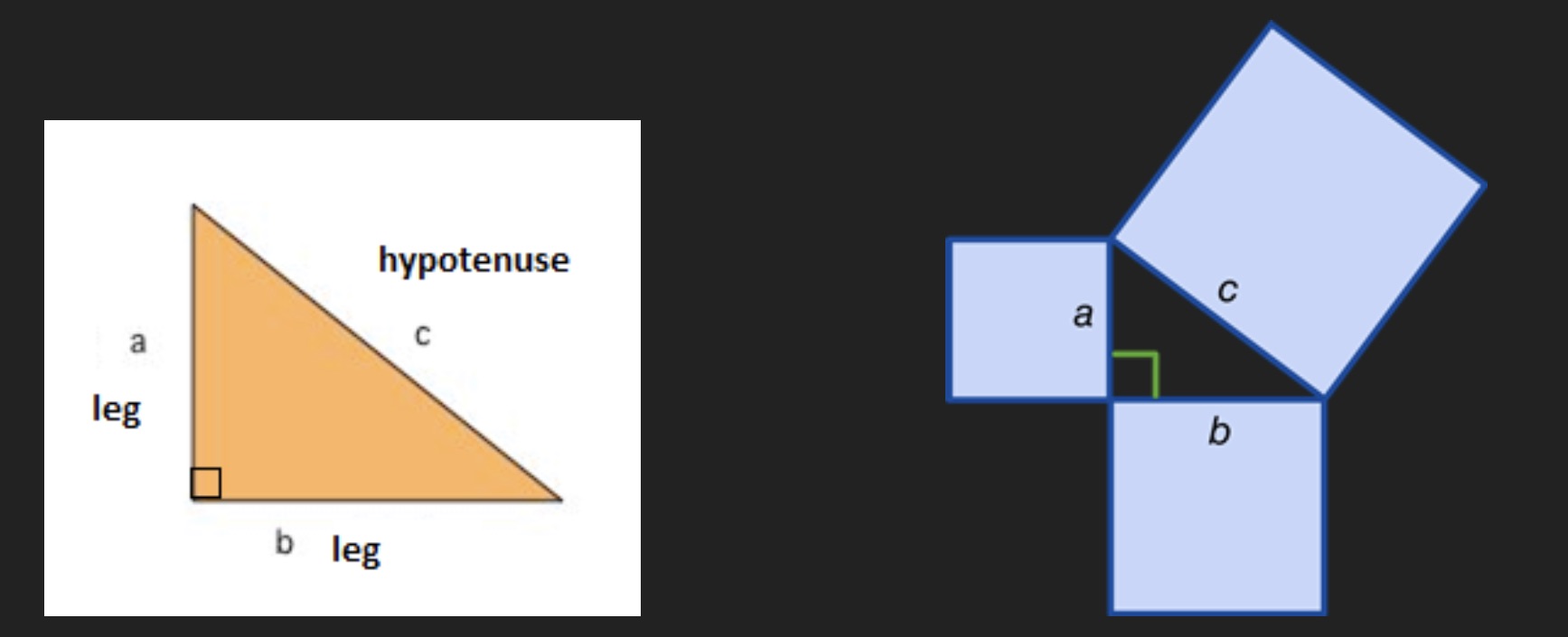The pythagorean theorem states that a2+b2=c2 or that the sum of the squares of the legs is equal to the square of the hypotenuse.
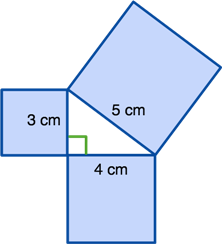
Example:
According to the pythagorean theorem:
a2+b2=c2= 32 + 42 = 52 = 9 + 16 = 25
The area of the two smaller squares is (3 × 3 = 9 cm2) and (4 × 4 = 16 cm2).
The area of the larger square is equal to (5 × 5 = 25 cm2).
If you add the two smaller areas together, you get the area of the square of the hypotenuse (9 + 16 = 25 cm2).
A QUADRILATERAL is a four sided polygon. A property unique to quadrilaterals is that they can have parallel opposite sides (have the same continuous distance between them).
A trapezoid is a type of quadrilateral with only one set of parallel sides.
A parallelogram is a type of quadrilateral whose two pairs of opposite sides are parallel, and as a result, the opposite sides are of equal length. Squares, rectangles, and rhombi are all parallelograms since their opposite sides are parallel.
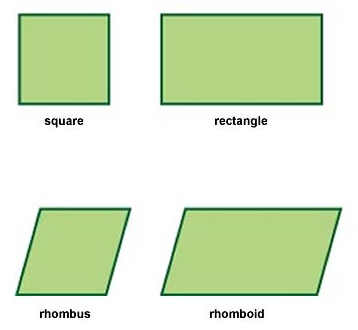
A rectangle is a type of parallelogram whose sides are perpendicular or meet at 90 degree angles.
A square is a special type of rectangle whose sides are all of equal length.
A rhomboid is a type of parallelogram whose sides do not meet at 90 degree.
A rhombus is a special type of type of rhomboid whose sides do not meet at 90 degree angles but are all of equal length.
TANGRAM FORMATION
The Tangram is a set of seven geometric shapes, also called tans, made up of five right isosceles triangles (two large, one medium, and two small), a square, and a rhomboid.
Let’s take a closer look at the specific shapes in a tangram and the relationships between them.
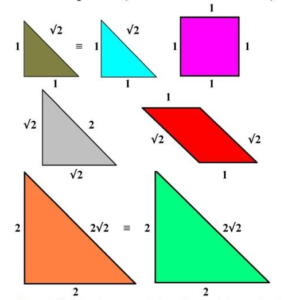
An interesting aspect of the tangram set is that all of the tangram pieces can be completely covered with the small tangram triangles. The small triangle is thus the unit of measure when comparing the areas of the tangram pieces.
Since the medium triangle, the square, and the rhomboid are each made up of two small tangram triangles, they each have an area 2x that of the small triangle. The large triangle is made up of four small tangram triangles and thus has an area 4x that of the small triangle and twice that of the other tangram pieces.
Another special aspect of the pieces is that all seven tans fit together to form a square. The individual tans can be defined by the number of small triangles that they are made up of (small triangle 1, small triangle 1, medium triangle 2, square 2, rhomboid 2, large square 4, large square 4; TOTAL=16 small triangles)
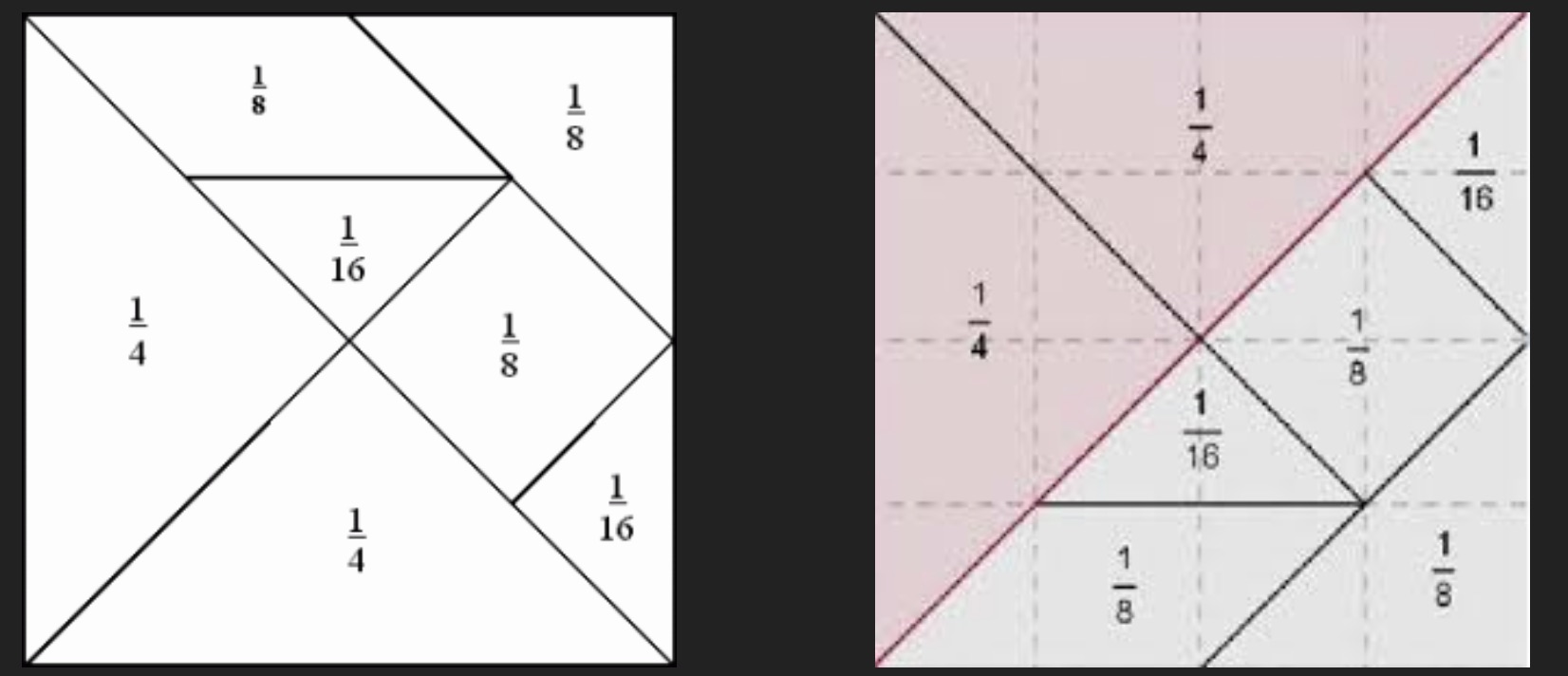
In this formation it is easy to imagine that the tangram is basically made up of 16 small triangles. From this we can correlate what fraction of the square area each of the tans comprises.
- The small triangles each form 1/16 of the square.
- The medium triangle forms ⅛ of the square.
- The square forms ⅛ of the square.
- The rhomboid forms ⅛ of the square.
- The large triangles each form ¼ of the square.
Following the Pythagorean Theorem and then a bit of deductive addition, we can calculate the relative lengths of the sides of each of the seven tans.
TANGRAMS AS POLYGONS
Remembering that a polygon is an enclosed, two-dimensional shape with more than two straight sides, we can ask ourselves if tangrams are polygons? Since proper tangrams consist of the seven tans touching without overlapping, then YES, tangrams are polygons.
Polygons, can be simple or complex.
A simple polygon is an enclosed shape consisting of straight, non-intersecting lines.
A complex polygon is an enclosed shape consisting of straight lines that intersect.
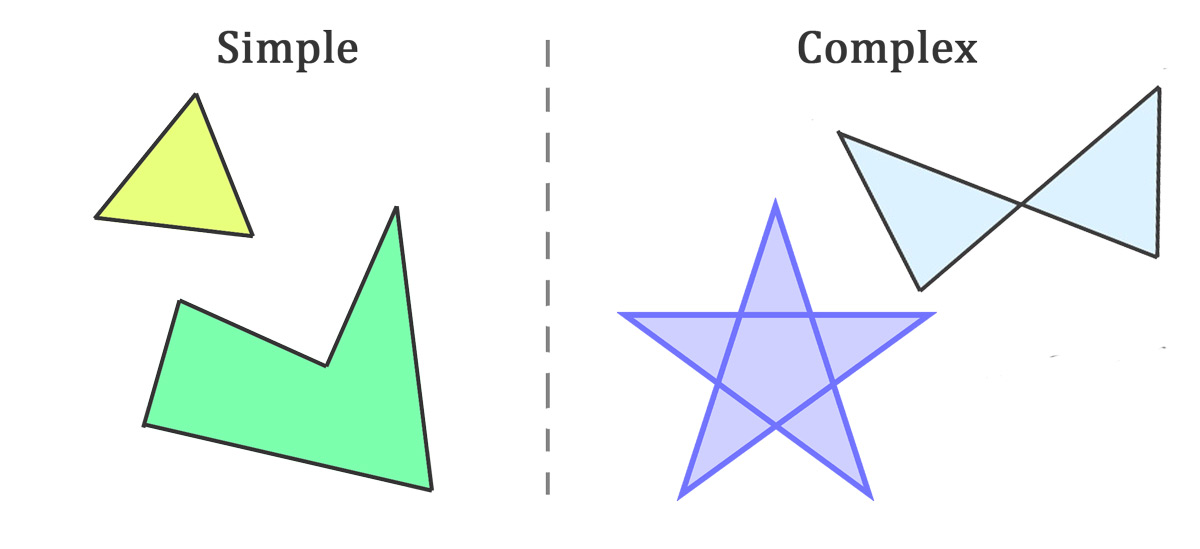
Tangrams do not overlap and so do not have lines that intersect. Tangrams are therefore, simple polygons. Like simple polygons, they can be concave or convex.
A concave polygon has one or more angles pointing inwards and therefore contains angles greater than 180°. Nearly all tangram configurations are concave.
A convex polygon has no angles pointing inwards. More precisely, no internal angle is greater than 180°. Of the thousands of existing tangram figures, there are only 13 convex tangram configurations.
