ROTATIONAL SYMMETRY
An object has rotational symmetry if, when you rotate it by a certain amount, the resulting image is identical to the original image – or the image coincides with itself.
The angle of rotational symmetry (or angle of symmetry) is the smallest angle by which you can rotate the image so that you produce an identically oriented figure.
For example, consider an equilateral triangle. An equilateral triangle is a triangle where all sides are of equal length, and all angles measure 60°. The smallest angle by which we can rotate such a triangle to get an equilateral triangle of the same orientation is 120°; therefore, the angle of symmetry of an equilateral triangle is 120°.
Notice that we can also rotate the equilateral triangle by 240°and 360° to produce the same result!
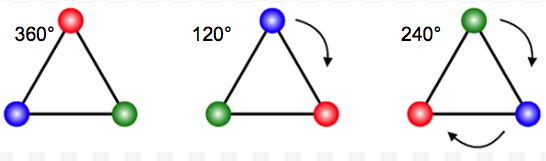
The order of rotational symmetry (or order of rotation) is the number of angles less than or equal to 360° by which we can rotate a shape to get an identically oriented shape.
It follows from the above diagram that the order of rotational symmetry of an equilateral triangle is 3 because there are exactly three angles less than or equal to 360° by which such a triangle can be rotated to coincide with itself (360°, 240° and 120°).
The order of rotational symmetry can be found by dividing 360 by the angle of rotational symmetry. In the triangle example: 360° ÷ 120° = 3.
REFLECTIVE SYMMETRY
An object is said to have reflective symmetry when a line can be drawn through some part of it, and the shapes on either side of the line are mirror images of each other. That is, if you placed a mirror on this line, and looked at the first half of the shape through the mirror, the resulting image would be identical to the second half.
The line of reflection is the line that divides these two mirror-image shapes. If you were to fold the image along the line of reflection, both sides would align perfectly.
For example, consider this butterfly:
The butterfly has reflective symmetry, because we can draw the dotted line through a part of the butterfly and the resulting pieces are mirror images of each other.
The total order of symmetry of an object is the sum of the object’s order of rotational symmetry and its number of lines of reflection.
Mandalas exhibit a lot of rotational and reflective symmetry.
Consider the mandala below in applying the concepts that we have just discussed: angle of rotation, order of rotation, lines of symmetry, and total order of symmetry.

This mandala’s angle of rotation is 45°. The smallest angle by which we can rotate the mandala to produce an identical configuration is 45°.
Its order of rotation is 360° ÷ 45° = 8. The number of angles less than or equal to 360° by which we can rotate the mandala to get the same image is 8.
We can also see that this mandala has 8 lines of reflection. Each of these 8 lines divide the mandala into mirror image halves.
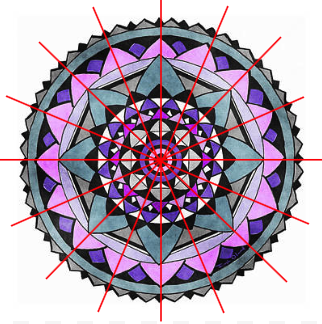
Therefore, the mandala’s total order of symmetry is equal to 8 + 8 = 16.
Pretty straight-forward!

